-- 发布时间:10/4/2006 10:07:00 PM
--
找到证明了。
由于有结论:
1、如果n阶矩阵C的特征值依次为λ_1, λ_2, ..., λ_n,那么E-C的特征值依次为1-λ_1, 1-λ_2, ..., 1-λ_n(这个结论在一般的线性代数书中都有证明)。
2、如果A是m*n阶矩阵,B是n*m阶矩阵(m≥n),则f_AB=λ^(m-n)f_BA。其中f_AB和f_BA分别是AB和BA的特征多项式。这一结论的证明见后(摘自陈大新的《矩阵理论》)。
由这两个结论就可以知道|E-AB|和|E-BA|对应的特征值完全相同,从而有|E-AB|=|E-BA|。
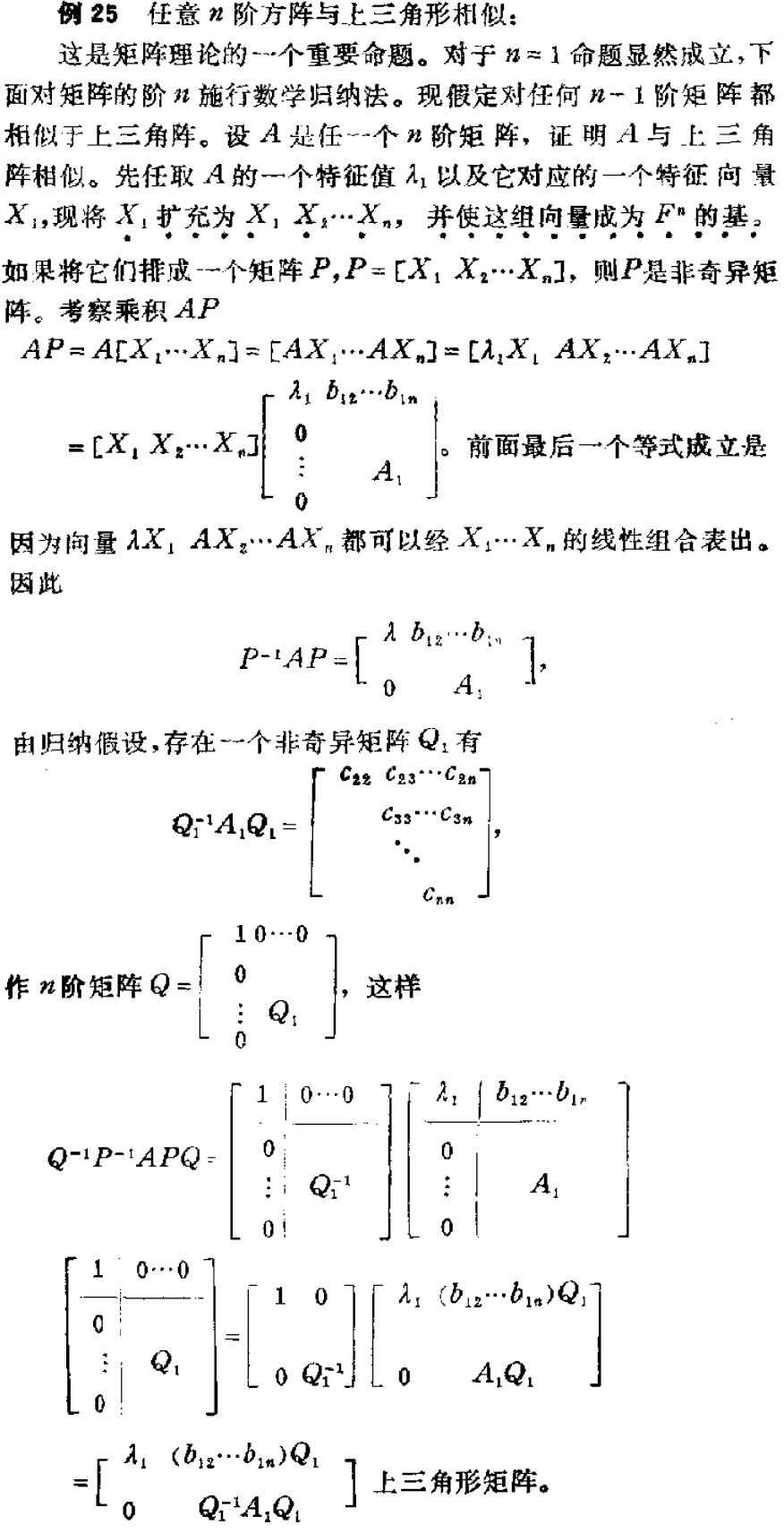
 此主题相关图片如下:
此主题相关图片如下: