-- 发布时间:12/3/2007 12:06:00 AM
--
用教材定理17.22,令H=G,b=e,即得Ga=G。
同理,由教材定理17.25,得aG=G。
 此主题相关图片如下:
此主题相关图片如下: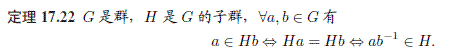
 此主题相关图片如下:
此主题相关图片如下: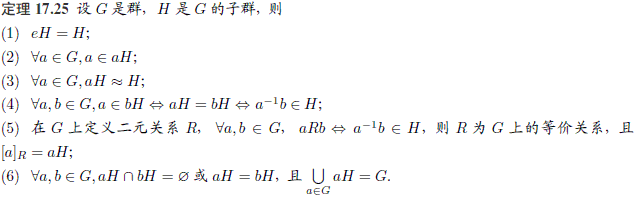
|
以文本方式查看主题 - 中文XML论坛 - 专业的XML技术讨论区 (http://bbs.xml.org.cn/index.asp) -- 『 计算机考研交流 』 (http://bbs.xml.org.cn/list.asp?boardid=67) ---- [求助] Logician老大请进来下,上次你说的那个定理书上没有啊?! (http://bbs.xml.org.cn/dispbbs.asp?boardid=67&rootid=&id=56274) |
|
-- 作者:fgffggfg -- 发布时间:12/2/2007 8:07:00 PM -- [求助] Logician老大请进来下,上次你说的那个定理书上没有啊?! 上次我问的那个离散问题, 老大你解答说:aG=G(由教材定理) 可是我把书翻了好几遍了就是没这个定理。 在p251定理17。6的证明中有这个写法: 令G={a1,a2....an} 任意a,ai属于G令aG={aai|i=1,2,...n} 则aG属于G。且可证aG中元素两两不同 所以aG中含n个元素,所以aG=G。 书上有关aG=G的就这里提到了,但是这个证明的前提是 G是有限群啊? 老大书上的定理在什么地方,或者怎么证明对无限群也成立啊? 谢谢拉~ |
|
-- 作者:zshao -- 发布时间:12/2/2007 10:35:00 PM -- 证明如下: 因为“G” 是“G”的平凡子群(当然也是子群)。 (1) (1)代入(2)。就可以有aG=G了。
请 Logician裁决下:》
|
|
-- 作者:Logician -- 发布时间:12/3/2007 12:06:00 AM -- 用教材定理17.22,令H=G,b=e,即得Ga=G。 同理,由教材定理17.25,得aG=G。  此主题相关图片如下: 此主题相关图片如下: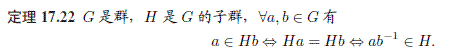  此主题相关图片如下: 此主题相关图片如下: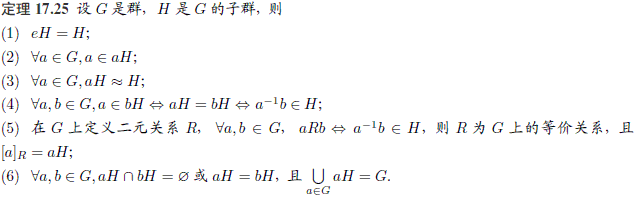
|
|
-- 作者:Logician -- 发布时间:12/3/2007 12:08:00 AM -- Nod.
|
|
-- 作者:Logician -- 发布时间:12/3/2007 12:13:00 AM -- By the way, 发帖最好不要用“请XXX进来看一下”这样的标题。 毕竟论坛是大家讨论的地方,标题应该给大家以更大的信息量(总结帖子的主题) 同时不应该限定某人回答,这样大家才有讨论的空间 版上的帖子我都会看,遇到我比较熟悉的问题(并且我有时间的话)我就会回答的…… :) |
|
-- 作者:zshao -- 发布时间:12/3/2007 12:38:00 AM --
|
|
-- 作者:fgffggfg -- 发布时间:12/3/2007 12:49:00 AM -- 谢谢老大了呵呵,因为翻了n遍书所以急了,还以为买了盗版书呢呵呵~ 不过老大说“由书上定理”,我还以为是由定理直接有aG=G呢呵呵, 没想还要证明1步~ btw“令H是G的子群,对于任意的a属于G,若a属于H,则aH=H。”这个定理书上也 |
|
-- 作者:Logician -- 发布时间:12/3/2007 2:26:00 AM -- “令H是G的子群,对于任意的a属于G,若a属于H,则aH=H。” 这不就是我说的那两个定理吗? 首先eH=H,这个是不用想的。 于是,定理17.22(或者说17.25(4))实际就是上述结论的推广 令b=e,就得到定理17.22的一个特例:a∈H <==> Ha=H <==> a^{-1}∈H 怎么看到了推广,却反而想不明白它的特例了呢?:) |
|
-- 作者:fgffggfg -- 发布时间:12/3/2007 10:54:00 PM -- 谢谢老大,我看明白了。 我是想问下,这样把特例代入定理中条件而得到的结论 考试时候可不可以直接用,还是也要简单说明一下? |
|
-- 作者:蝶影 -- 发布时间:12/3/2007 10:54:00 PM -- “令H是G的子群,对于任意的a属于G,若a属于H,则aH=H。” 其实一开始我做题的时候,也没反应过来,问问题的时候,还被人说了一下...... |
|
-- 作者:Logician -- 发布时间:12/3/2007 11:54:00 PM -- 我觉得不用,代数重思想(不像集合论或逻辑,极端重严格),你直接写"aG=G"我觉得都没有问题。稍微严格一点,就按zshao的方式写肯定没问题了。 |
|
-- 作者:fgffggfg -- 发布时间:12/5/2007 12:07:00 AM -- 不能怪偶们呵呵,教材这里只字未提就出来aG=Ga了~ |
|
W 3 C h i n a ( since 2003 ) 旗 下 站 点 苏ICP备05006046号《全国人大常委会关于维护互联网安全的决定》《计算机信息网络国际联网安全保护管理办法》 |
62.500ms |